Photonics evolution has urgently posed the necessity to deal with manufacturing variability which often limits the sustainable complexity and poses major problems in achieving high production yield. This is particularly true for high-index-contrast technologies as silicon-on-insulator where small fabrication deviations in the waveguide geometry and circuit topology, optical and thermal interactions between single devices, spurious effects, drifts, and non-idealities can have significant impacts on light propagation. Tolerance analysis is hence becoming central to predict the effects of fabrication uncertainties on the behavior of the devices and circuits and to take these effects into account during early design stages.
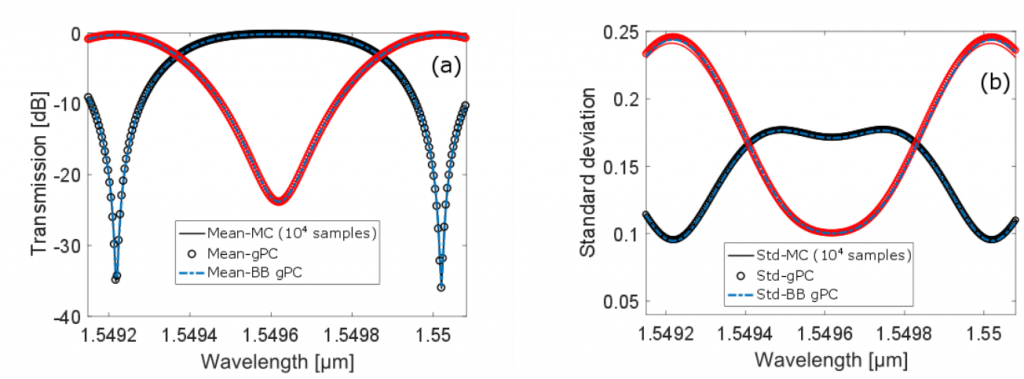
Monte Carlo is a robust, accurate, and easy-to-implement approach, and is often considered as the standard for stochastic analysis. However, the high computational cost can hamper its application to the analysis of even relatively simple circuits because a large number of simulation runs (generally in the order of 104-105) is required to obtain reliable results. For these reason, stochastic spectral methods are investigated in several application fields, including photonics, as an efficient alternative to the classical Monte Carlo method for stochastic analysis. The core idea of these techniques, in particular the generalized polynomial chaos (gPC) expansion method, is to efficiently generate an inexpensive “surrogate” model that approximates the dependence of a simulation output on the stochastic input parameters. This avoids running for thousands of times an expensive simulator with random inputs, vastly reducing the computational time required to obtain stochastic information on the behaviour of devices and circuits.
Stochastic optimization
The availability of information on manufacturing variability during the design phase and the use of efficient tools as polynomial chaos expansion allows to go beyond the sole prediction of tolerance effects, opening the possibility to include variability in the design process and generate optimized layouts.
The tricky aspect in the optimization of a stochastic quantity (i.e. the maximization of a circuit fabrication yield under manufacturing variability) is that the computation of this quantity is often required at each step of the optimization algorithm and this is normally lengthy and time consuming. In this case polynomial chaos expansion can be of great help. Approximated models can be used for both the objective function and the constraints, ensuring a computational time thousands of times faster than the direct use of Monte Carlo approach.
Stochastic Process Design Kits
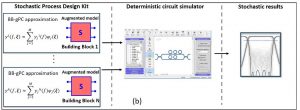Process Design Kits (PDKs) are an indispensable tool for the analysis and design of complex circuits. A PDK contains a large amount of foundry-specific information that can be used to design, simulate and fabricate circuits exploiting a given fabrication technology.
Generalized polynomial chaos expansion can be utilized to realize a completely novel class of device models to be used within photonic PDKs. Stochastic collocation and stochastic Galerkin are combined to build augmented macro-models of each building block, directly embedding stochastic information in the form of gPC coefficients. These stochastic macro-models, in the form of transmission or scattering matrices, are circuit independent and can be stored and replace the original deterministic macro-model of the building blocks typically included in the PDK. The new matrices can be combined according to the building blocks connections to derive with a single run of the deterministic circuit simulator the stochastic behaviour of any circuit.
P. Manfredi, A. Waqas, and D. Melati, ‘Stochastic and multi-objective design of photonic devices with machine learning’, Sci Rep, vol. 14, no. 1, p. 7162, Mar. 2024, doi: 10.1038/s41598-024-57315-4.
A. Waqas, P. Manfredi, and D. Melati, ‘Performance Variability Analysis of Photonic Circuits With Many Correlated Parameters’, Journal of Lightwave Technology, vol. 39, no. 14, pp. 4737–4744, Jul. 2021, doi: 10.1109/JLT.2021.3076023.
A. Waqas, D. Melati, B. S. Chowdhry, and A. Melloni, ‘Efficient variability analysis of photonic circuits by stochastic parametric building blocks’, IEEE Journal of Selected Topics in Quantum Electronics, pp. 1–1, Mar. 2020, doi: 10.1109/JSTQE.2019.2950761.